Bewertung des Infektionsrisikos durch analytische Methoden
Zur Minderung des Infektionsrisikos durch SARS-CoV-2 veröffentlichten internationale und nationale Organisationen Vorschläge und Richtlinien, die sowohl lüftungstechnische als auch nicht-lüftungstechnische Maßnahmen beinhalteten. Allen Empfehlungen gemein ist, dass so viel Frischluft wie möglich von außen zugeführt und damit virenhaltige Luft abgeführt werden sollte. Der Bewertung des Infektionsrisikos kommt in diesem Zusammenhang eine besondere Bedeutung zu, die dabei helfen kann, die Effizienz der entsprechenden Infektionskontrollstrategien zu quantifizieren und zu bewerten. Durch die gängigen Risikobewertungsmethoden können Empfehlungen eingeordnet werden. Im Folgenden wird der analytische Ansatz vorgestellt.
Das Dosis-Wirkungs-Modell
Eine Abschätzung des Infektionsrisikos durch Luftübertragung ermöglicht ein einfacher analytischer Ansatz. Hierbei wird über das gesamte Raumvolumen bilanziert, und es wird eine homogene, das heißt gleichmäßige, Verteilung der Erreger in der Raumluft angenommen. Dazu wird die Emissionsrate ins Verhältnis zur Eliminierungsrate gesetzt. Je höher die Emissionsrate, desto höher muss die Eliminierungsrate sein, und je höher die Eliminierungsrate, desto niedriger ist die Anzahl der sich in der Raumluft aufhaltenden Erreger.
Das Dosis-Wirkungs-Modell, z. B. Wells-Riley-Modell, ist eine analytische Methode, die zur Quantifizierung des Risikos einer luftübertragenen Infektion verwendet werden kann. Das Wells-Riley-Modell, siehe Gleichung 1, verwendet das Konzept des Infektionsquantums, das eine fiktive Größe ist, um die Infektionswahrscheinlichkeit P (%) auf der Grundlage der Poisson-Wahrscheinlichkeitsverteilung zu berechnen.
\( P = \frac{C}{S} = 1-e^{-(\frac{Iqpt}{Q})} \) (1)
Hierbei ist C die Anzahl der Infektionsfälle, S die Anzahl der exponierten Personen, I die Anzahl der infektiösen Personen, q (1/h) die Quanta, p (m3/h) die Atmungsrate der exponierten Personen, Q (m3/h) der dem Raum zu- und abgeführte Luftvolumenstrom (Lüftungsrate des Raums) und t (h) die Expositionszeit. Quanta q hängt von der Infektiosität des Virus, der Viruslast in den aerosolproduzierenden Regionen des Körpers (Atemwege), der Aerosolproduktionsrate (Anzahl und Größenverteilung) und den natürlichen Schutzfunktionen (z. B. Immunantwort und Abscheideeffizienz über Sekret in den Atemwegen) bei der exponierten Person ab und ist somit im Allgemeinen unbekannt. Neben dem Quanta gehören zu den wichtigsten Nachteilen dieses Modells die Annahme einer ideal durchmischten Luft und der angenommene stationäre Zustand (zeitunabhängig). Das Modell nimmt also an, dass die von einer infizierten Person emittierten Erreger unmittelbar nach dem Verlassen der Atemwege überall im Raum gleich verteilt sind und sich zusammen mit der Eliminierungsrate somit im Raum eine einheitliche Konzentration an Erregern (Anzahl pro Kubikmeter) sofort überall einstellt.
In einer Arbeit von Kriegel et al., 2021, wird detailliert auf die einzelnen Parameter eines Dosis-Wirkungs-Modells eingegangen, mehrere tatsächliche Ausbrüche werden analysiert, und die Wirkung von Infektionspräventionsmaßnahmen wird bewertet. Hieraus lassen sich einfach anzuwendende Gleichungen zur Berechnung von Infektionswahrscheinlichkeiten entnehmen und weiter ableiten.
Die situationsbedingte Reproduktionszahl
Statistisch kann davon ausgegangen werden, dass die prozentuale Ansteckungsrate (Attack Rate) einer sich innerhalb derselben Situation aufhaltenden Personengruppe dem individuellen Risiko gleicht. Wenn nun die Anzahl der sich in der Situation befindenden Personen S multipliziert wird mit dem Infektionsrisiko P, resultiert C, die Anzahl der Infektionsfälle. Diese Zahl kann auch als situationsbedingter R-Wert RS (Reproduktionszahl; die Anzahl der sich in der betrachteten Situation ansteckenden Personen) definiert werden.
Die bereits genannte Gleichung 1 zur Berechnung von P und RS kann mathematisch vereinfacht werden zu den Gleichungen 2 und 3. Hierin ist VF der Virusfaktor, der sich aus oben genannter Arbeit ergibt und dem Quanta q aus Gleichung 1 entspricht. n ist die Gesamtpersonenanzahl (Exponierte S + Infizierte I). Der dem Raum zu- und abgeführte Luftvolumenstrom Q kann personenbezogen ausgedrückt werden mittels qPers = Q/n.
\( P = V_F \cdot \frac{t}{q_{pers} \cdot n} \cdot p \) (2)
\( R_S = V_F \cdot \frac{t}{q_{pers}} \cdot p \) (3)
\( q_{pers} = \frac{C_{exh}}{C_R – C_0} \cdot p \) (4)
Der personenbezogene Luftvolumenstrom korreliert über Gleichung 4 mit dem CO2-Gehalt in der Raumluft. Damit ist es möglich, einen direkten Zusammenhang zwischen P und RS und dem CO2-Gehalt in der Raumluft darzustellen. Hier ist Cexh die CO2-Konzentration in der Ausatemluft (ca. 40.000 ppm), CR der CO2-Gehalt in der Raumluft und C0 die CO2-Konzentration in der dem Raum zugeführten Außenluft (ca. 400–450 ppm).
Daraus folgt für die situationsbedingte Reproduktionszahl Gleichung 5.
\( R_S = V_F \cdot \frac{t \cdot (C_R – C_O)}{\frac{40.000ppm}{Pers}} \) (5)
Das relative Infektionsrisiko
Da insbesondere der Virusfaktor VF nicht exakt bestimmt werden kann und darüber hinaus personenabhängig ist, eignen sich für Bewertungen der Effektivität von lüftungstechnischen Maßnahmen relative Betrachtungen.
Das Verhältnis zweier Situationen zueinander wird durch den Risikofaktor xr aus Kriegel et al. abgebildet (siehe Gleichung 6). Wird Gleichung 5 hierin eingesetzt und davon ausgegangen, dass außer der CO2-Konzentrationen in der Raumluft alle weiteren Variablen in beiden betrachteten Lüftungsszenarien übereinstimmen, ergibt sich Gleichung 7.
\( x_r = \frac{R_{s,2}}{R_{S,1}} \) (6)
\( = \frac {(C_{R,2}-C_O)}{(C_{R,1}-C_O)} \) (7)
Bisher wird in dieser Betrachtung die Lüftungsmethode außer Acht gelassen. Sie kann über die Lüftungseffektivität \(\varepsilon_{\nu} \) nach DIN EN 16798-3:2017-11 hinzugefügt werden (siehe Gleichung 8). Durch Einsetzen in Gleichung 7 ergibt sich Gleichung 9.
\( \varepsilon_{\nu} = \frac{C_e – C_S}{C_i – C_S} \) (8)
\( x_r = \frac{\frac{(C_{R,2} – C_O)}{\varepsilon_{\nu,2}}}{\frac{(C_{R,1} – C_O)}{\varepsilon_{\nu,1}}} \) (9)
Wichtiger Hinweis!
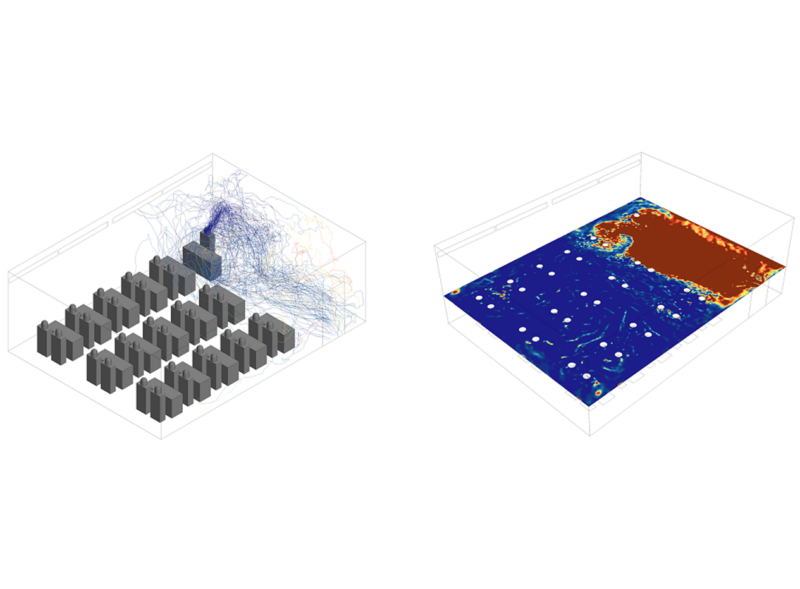
Obwohl mathematische Modelle ein einfaches und schnelles Verfahren zur Bewertung von Maßnahmen zur Infektionskontrolle sind, beschränkt sich die Bedeutung eines Übertragungsereignisses nicht allein auf die Belüftungs- und die Filtrations- bzw. Eliminierungsrate des gesamten Raumes, sondern umfasst auch die Luftstromrichtung und die Luftstrommuster. Die Verteilung von Viren in einem Raum und damit die von Personen inhalierte Dosis werden durch diese beiden Faktoren beeinflusst. Diese Aspekte sind zu komplex, um sie in einfachen analytischen Modellen berücksichtigen zu können. Umfangreichere numerische Methoden und/oder groß angelegte Experimente sind erforderlich, um detaillierte Aussagen zum Ausbreitungsverhalten der Erreger und des Infektionsrisikos in einer speziellen Situation zu treffen.
🚧 Rechenbeispiel: Vergleichende Bewertung
Der Risikofaktor wurde beispielhaft für einige Lüftungsszenarien berechnet. Für das Referenzszenario wurden folgende Randbedingungen angenommen:
- Die Innenraumkonzentration an CO2 beträgt 1000 ppm.
- Es wird ideale Mischlüftung genutzt. Die Lüftungseffektivität nach VDI 3804:2009-03 beträgt hierfür \( \varepsilon_{\nu,1} = 1 \).
Die CO2-Konzentration der Außenluft wird in allen Fällen mit 450 ppm angenommen.
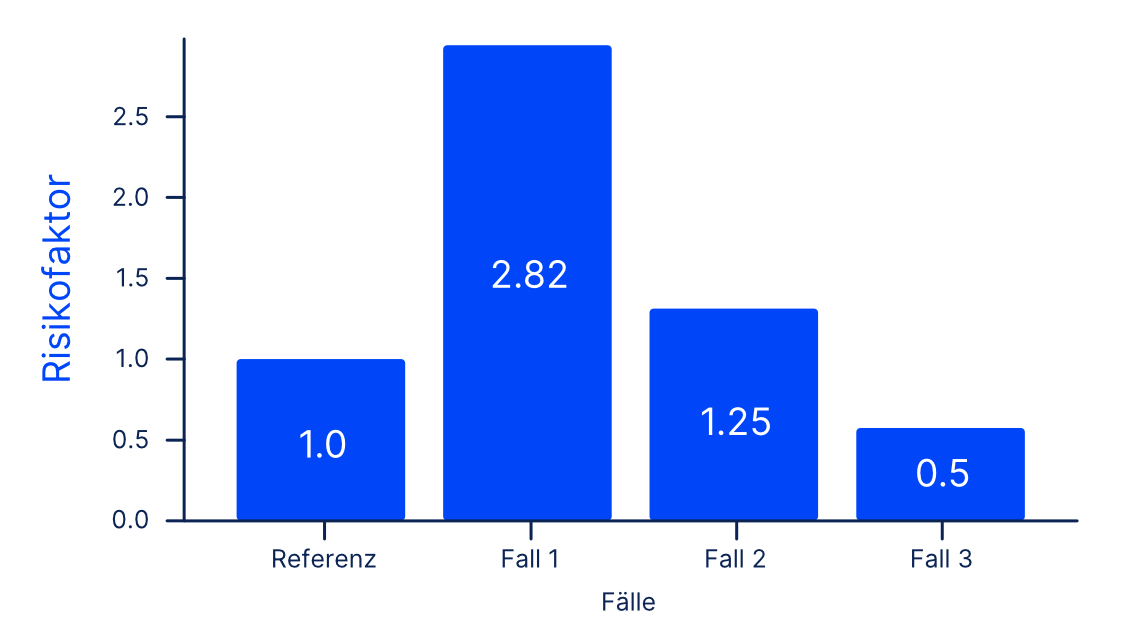
Folgende drei Fälle wurden unabhängig von der Raumnutzungsart betrachtet und zur Referenzsituation ins Verhältnis gesetzt:
1. Die CO2-Konzentration in der Innenraumluft beträgt 2000 ppm.
2. Die Mischlüftung ist nicht ideal, d.h. \( \varepsilon_{\nu,2} = 0,8 \).
3. Es wird Quell- statt Mischlüftung genutzt, d.h. \( \varepsilon_{\nu,2} = 2 \).
Den größten Einfluss auf die Änderung des Risikofaktors hat die Erhöhung der CO2-Konzentration im Innneraum auf 2000 ppm. Der Risikofaktor erhöht sich hierdurch um fast das 3-fache auf 2,82. In Fall 2 liegt der Risikofaktor bei 1,25, in Fall 3 reduziert er sich um 50% auf 0,5. Die Ergebnisse sind in Abbildung 1 dargestellt.